How to Square a Foundation Using Simple Construction Math
Oct 20, 2020
A solid house begins with a properly constructed foundation, and common to almost all of them is that they have right angles at their corners. (Note: If you are building a fun house or an avant-garde building, some common rules may not apply.) If the corners of your foundation stray too far from right angles, then beams, joists, and other structural supports will fit together only loosely—or not at all. A corner with a right angle is known as perfectly “square.”
The first step to laying out most larger foundations is to set up batter’s boards (these are, simply, stakes with horizontal crosspieces) in the corners just beyond where the foundation will sit. You’ll then use the batter’s boards as guides to where you will string lines along what will be the edges of the foundation.
These guidelines will help you determine the exact locations where you’ll want to construct forms for the foundation.
How to Guarantee Your Corners Are Square
When it comes time to stake out the foundation and assure that all the angles are right, (or 90-degrees), professional builder and craftsman Jordan Smith turns to two time-tested methods—in fact, they date back to ancient Greece.
Pythagorean Theorem Method
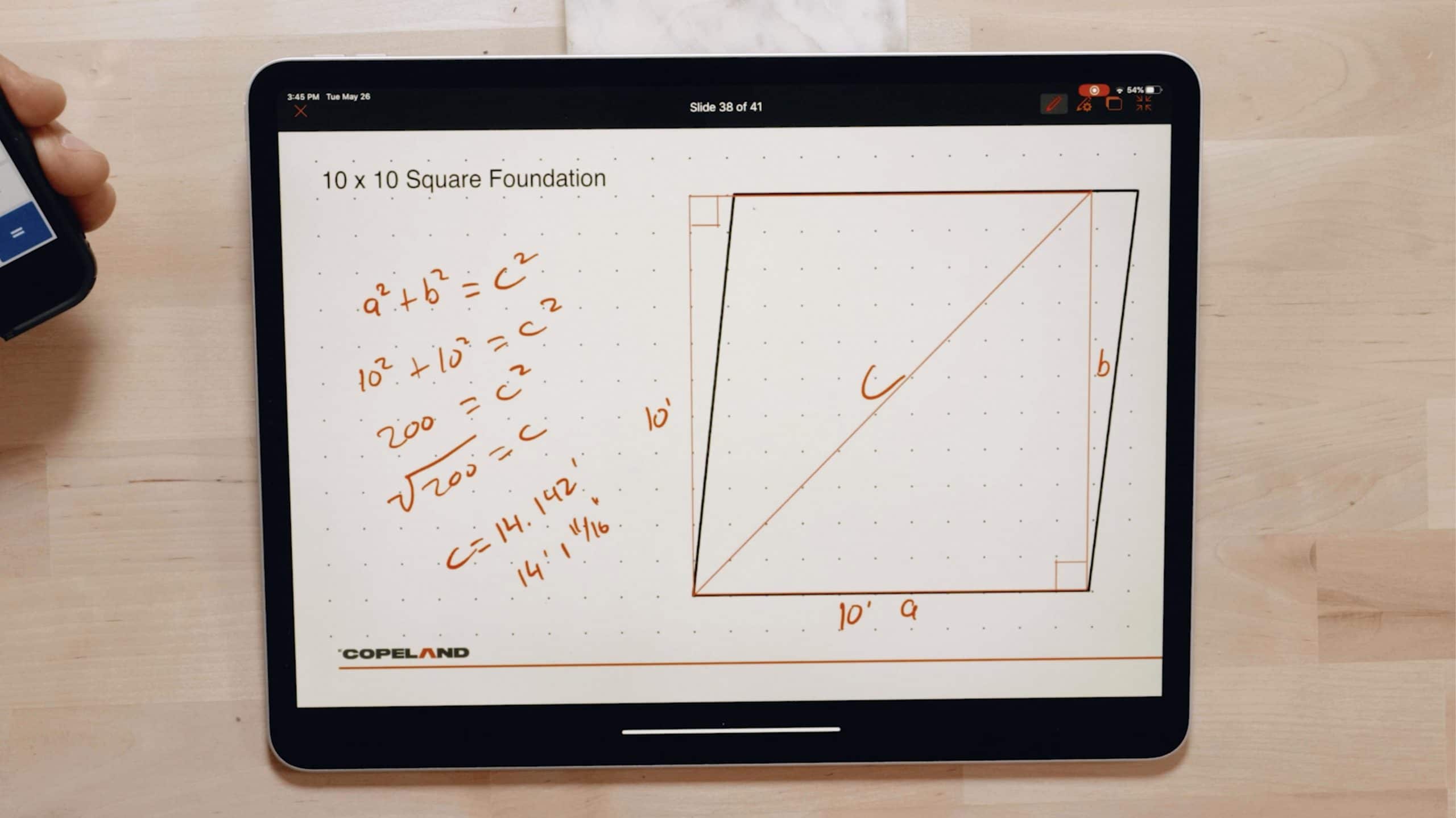
Sixth-century BC philosopher Pythagoras is best-known for his eponymous theorem: a2+ b2=c2. In other words, according to the Pythagorean Theorem, in a right triangle if you add together the squares of the lengths of the two shorter sides, they will equal the square of the hypotenuse (the longest side of a right triangle).
Here’s how this theorem applies to squaring a foundation. Say you are laying the foundation of a square room with 10-foot long walls on each side. Think of the room as two separate right triangles. The diagonal that cuts across the room, and which forms the hypotenuse of the triangles, should be 14.142 feet: 102+102=200. The square root of 200 is 14.142 feet. (For easier measuring, you can convert this to 14 feet and 1 11/16 inches.)
If the hypotenuse is longer than 14.142 feet, it means that the angle at the corner of the room is greater than 90 degrees. If it is less than 14.142 feet, then the angle is less than 90 degrees.
A solid house begins with a properly constructed foundation, and common to almost all of them is that they have right angles at their corners. (Note: If you are building a fun house or an avant-garde building, some common rules may not apply.) If the corners of your foundation stray too far from right angles, then beams, joists, and other structural supports will fit together only loosely—or not at all. A corner with a right angle is known as perfectly “square.”
The first step to laying out most larger foundations is to set up batter’s boards (these are, simply, stakes with horizontal crosspieces) in the corners just beyond where the foundation will sit. You’ll then use the batter’s boards as guides to where you will string lines along what will be the edges of the foundation.
These guidelines will help you determine the exact locations where you’ll want to construct forms for the foundation.
How to Guarantee Your Corners Are Square
When it comes time to stake out the foundation and assure that all the angles are right, (or 90-degrees), professional builder and craftsman Jordan Smith turns to two time-tested methods—in fact, they date back to ancient Greece.
Pythagorean Theorem Method
Sixth-century BC philosopher Pythagoras is best-known for his eponymous theorem: a2+ b2=c2. In other words, according to the Pythagorean Theorem, in a right triangle if you add together the squares of the lengths of the two shorter sides, they will equal the square of the hypotenuse (the longest side of a right triangle).
Here’s how this theorem applies to squaring a foundation. Say you are laying the foundation of a square room with 10-foot long walls on each side. Think of the room as two separate right triangles. The diagonal that cuts across the room, and which forms the hypotenuse of the triangles, should be 14.142 feet: 102+102=200. The square root of 200 is 14.142 feet. (For easier measuring, you can convert this to 14 feet and 1 11/16 inches.)
If the hypotenuse is longer than 14.142 feet, it means that the angle at the corner of the room is greater than 90 degrees. If it is less than 14.142 feet, then the angle is less than 90 degrees.
Understanding basic construction math will help you execute every project more quickly and easily. Learn the fundamentals—including fractions, geometry, and trigonometry—in MT Copeland’s online Construction Math class.
The 3-4-5 Method
Though it has a different name, this formula is based on the same theorem. The numbers in the method’s name provide an easy way to remember Pythagoras’s insight and they refer to the sides of a hypothetical right triangle. If the shorter sides are 3 feet and 4 feet, then the hypotenuse will be 5 feet. (We can test the numbers using Pythagoras’s theorem: 32+42=52. 3×3=9. 4×4=16. 5×5=25. And 9+16=25.)
To use this method to square any corner, you’ll measure the distances of 3 feet and 4 feet along the perpendicular walls, starting from the planned corner of the foundations, draw a line connecting their ends to form the hypotenuse. If it is greater than 5 feet, then the angle of the corner of the room is greater than 90 degrees. If it is shorter than 5 feet, then the angle is less than 90 degrees.
It is smart to repeat this test farther out along the walls: Is the line that connects the 6-foot point on one wall with the 8-foot point on the perpendicular one 10 feet long? If not, you’ll have to adjust your guidelines or forms.
After checking the angles of the planned corners of the foundation, don’t put the tape measure away yet. You’ll also want to confirm that the lengths of all the sides of the foundation are correct. While mistakes can be corrected after a foundation is poured, it’s always better (and cheaper) to avoid making them in the first place.
MT Copeland offers video-based online classes that give you a foundation in construction fundamentals with real-world applications. Classes include professionally produced videos taught by practicing craftspeople, and supplementary downloads like quizzes, blueprints, and other materials to help you master the skills.
Featured Instructor
Jordan Smith
Jordan Smith is the CEO and Founder of Smith House Company, a design+build firm based in Austin, Texas. He learned to build and weld while working on the farm with his grandad, and after earning a degree in Welding and Materials Engineering, he spent the next 10 years working in the heavy construction building everything from robots to ships to offshore oil rigs before transitioning to residential construction. After spending a couple of years working with industry leading builders in Austin, Jordan and his wife Veronica struck out on their own to form Smith House Co. Smith House Co. strives to build more beautiful, functional and resilient spaces which are self sustaining and harmonize with their natural surroundings.
Explore Classes
